A Fast and Accurate Unconstrained Face Detector 论文学习记录：NPD特征的应用

论文标题

• A Fast and Accurate Unconstrained Face Detector

论文地址

• https://ieeexplore.ieee.org/document/7130626/figures

论文代码

• http://www.cbsr.ia.ac.cn/users/scliao/projects/npdface/

论文摘要

We propose a method to address challenges in unconstrained face detection, such as arbitrary pose variations and occlusions. First, a new image feature called Normalized Pixel Difference (NPD) is proposed. NPD feature is computed as the difference to sum ratio between two pixel values, inspired by the Weber Fraction in experimental psychology. The new feature is scale invariant, bounded, and is able to reconstruct the original image. Second, we propose a deep quadratic tree to learn the optimal subset of NPD features and their combinations, so that complex face manifolds can be partitioned by the learned rules. This way, only a single soft-cascade classifier is needed to handle unconstrained face detection. Furthermore, we show that the NPD features can be efficiently obtained from a look up table, and the detection template can be easily scaled, making the proposed face detector very fast. Experimental results on three public face datasets (FDDB, GENKI, and CMU-MIT) show that the proposed method achieves state-of-the-art performance in detecting unconstrained faces with arbitrary pose variations and occlusions in cluttered scenes.

涉及数据集

• AFLW
• CMU-MIT
• FDDB
• GENKI

个人心得

• 该文章主要介绍了其引入的一个新特征NPD，Normalized Pixel Difference，并且利用深度二叉树来学习NPD特征的子集，而且检测模板能够容易地缩放以适应不同的图片。这个特征所具有的多个特点，能够有效地将图片中的像素间信息提取出来，以便于后续深度二叉树的建立。

NPD特征

• NPD（Normalized Pixel Difference）是文章中引入的一种特征，具有多个理想属性，包括尺度不变性、有界性与能够重建原始图像的能力。
• NPD特征是从韦伯分数（Weber Fraction）中启发而来的，韦伯分数的介绍如下：

韦伯分数，也称韦伯常数，德国生理学家韦伯（Weber，E.H.)1840年测量了重量的差别阈限，发现差别阈限和原来刺激强度的比例是一个常数，用公式表示就是△I/I=K。其中，△I是差别阈限，I是原来的刺激强度，K是一个常数，这个常数就叫韦伯分数，这个定律就是韦伯定律。

• 由韦伯分数中，启发的归一化像素特征差异可以解释为两个像素强度之间的差与它们的值之和的比值，用数学公式表示为

$$f(x,y)=\frac{x-y{}}{x+y} \tag{1}$$

• 其中 $x,y$≥$0$，代表了两个像素的强度值，$f(0,0)$被定义为定$0$。

• NPD的公式中具有几个特点：

  1. $f(x,y)$的符号表示了两个像素$x,y$的有序关系
  2. $f(x,y)$的大小衡量了$x,y$的相对差异
  3. $f(0,0)$是有意义的
  4. $f(x,y)$或$f(y,x)$都足够用于特征表示
  5. $f(x,y)$的边界在[-1,1]，有界属性使得NPD特征适合于直方图合并与阈值学习
• NPD函数的图像如下：
  
• 值得注意的是，有序关系是一种用于目标检测和识别的有效编码，因为有序关系对目标图像的固有结构进行了编码，并且在各种光照变化下它都是不变的。
• 当x与y的值接近时，噪声可能产生更大的影响

深度二叉树

• 由于Viola-Jones的浅层结构无法捕获不同特征维度之间的相互作用，而且简单的阈值处理也可能会忽略高阶信息，因此在该文章中作者提出了二分策略与更深的树结构。即对于特征x，树节点的分裂为
  $$(ax^{2}+bx+c)<t \tag{2}$$
• 其中$a$，$b$，$c$是关于$x$的常数，$t$是分割阈值。使用适当的系数，这相当于检查$x$是否在[$θ_{1}$，$θ_{2}$]范围内，其中$θ_{1}$和$θ_{2}$是两个学习出的阈值。
• 对于提出的NPD特征，可以学习三种对目标结构：

$$-1 \leq \frac{{}x-y}{x+y} \leq θ<0 \tag{3}$$

$$0 < θ \leq \frac{{}x-y}{x+y} \leq 1 \tag{4}$$

$$θ_{1} \leq \frac{{}x-y}{x+y} \leq θ_{2} \tag{5}$$

• 其中$θ_{1}$＜0且$θ_{2}$＞0。

• 如果目标像素x明显比像素y暗, 则使用等式（3），等式（4）涵盖了像素x明显比像素y亮的情况，这两种结构也可以通过经典决策桩学习。如果等式（5）不成立，则像素x和y之间会有明显的边缘或对比度。
• 应用二分可以来学习一棵深度二叉树，将几个NPD特征最佳地组合在一起表示固有的面部结构。由于相似的视图可以聚集在树的相同叶节点中，因此提出的深度二叉树非常适合于具有任意姿势变化的面部检测。

附录

• 该模型检测出的人脸
  
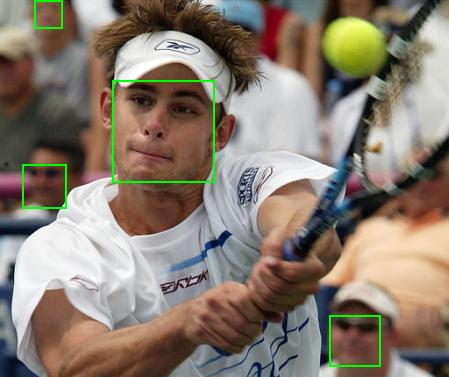
• 与FDDB数据集中标记对比