机器视觉-Chapter 3.2 Image Enhancement图像增强
3.2 Image Enhancement
3.2.1 Gray Value Transformations 灰度变换
- 调整图像灰度值的一个原因是由于图像对比度太弱,这个问题通常只会局部发生,只需增强局部的对比度;
另一个原因是图像的对比度或者亮度同最初系统设定时相比已经发生了变化
- 如:工作一段时间后由于光源的老化而造成图像对比度变弱
灰度值变换可以被视为一种点处理。
- 这意味着变换后的灰度值$t_{r,c}$仅仅依赖于图像上同一位置的原始灰度值$g_{r,c}:t_{r,c}=f(g_{r,c})$。$f$表示进行灰度值变换的函数,其值域范围通常是$G_{b}$,为离散的。
- 灰度值变换通常通过查找表(lookup table,LUT) 进行,即将每个输入灰度值变换后得到的输出值保存在这个查找表内。
3.2.1.1 Contrast Enhancement 对比度增强
最重要的灰度值变换是灰度值先行比例缩放:$f(g)=ag+b$,若$g∈G_{b}$,我们需要保证输出灰度值也在$G_{b}$内。所以按下式对输出灰度值进行裁剪和四舍五入处理:
- $f(g)=min(max(\lfloor ag+b+0.5\rfloor,0),2^{b}-1)$
- 当$|a|>1$时,对比度增加;当$|a|<1$时,对比度降低
- 当$a<0$时,灰度值反转
- $b>0$时,亮度增加,$b<0$时,亮度降低


- (a) Original image.
- (b) Decreased brightness (b = −50).
- (c) Increased brightness (b = 50).
- (d) Decreased contrast (a = 0.5).
- (e) Increased contrast (a = 2).
3.2.1.2 Contrast Normalization
- 希望有一种基于当前图像情况自动确定a和b的方法。
一种显而易见的方法时通过设置参数让变换后的图像灰度值覆盖$G_{b}$的最大取值范围。
- 用$g_{min}$和$g_{max}$分别保存当前ROI图像中的最小灰度值和最大灰度值
- 当$a=(2^{b}-1)/(g_{max}-g_{min})$且$b=-ag_{min}$时转换后的输出灰度值可以覆盖$G_{b}$的最大取值范围。
- 这种变换可以理解为灰度值的归一化处理
- (f) 灰度值归一化处理

3.2.1.3 Robust Contrast Normalization
- 如果图像中存在一个非常亮或非常暗的像素值,通过上述的灰度值归一化处理无法得到想要的灰度值范围。
- 灰度值直方图表示灰度值$i$出现的概率密度
$$h_{i}=\frac{n_{i}}{n}$$ - 累积直方图:
$$c_{i} = \sum_{j=0}^{i}h_{j}$$
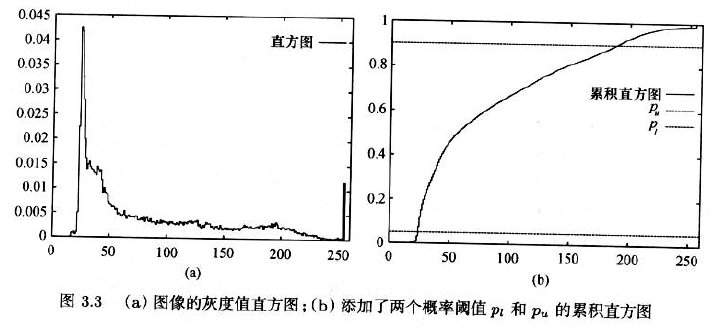
- 要得到鲁棒的灰度值归一化处理方法,只需要忽略直方图中包含的一小部分最暗的灰度值以及一小部分最亮的灰度值即可。
- 再累积直方图中设定$c_{i}\geq p_{i}$来确定最小灰度值,设定$c_{i}\leq p_{u}$来确定最大灰度值
- (g) shows the result that is obtained with pl = 0 and pu = 0.8. This improves the contrast of the components significantly.

3.2.2 Radiometric Calibration 辐射标定
很多图像处理算法时建立在传感器收集的能量和图像灰度值之间存在线性相应这一事实基础上的:$G=aE+b$
- $E$是传感器积累到的能量,$G$是图像上的灰度值
- 理想情况下$b=0$,这意味着传感器上两倍的能量会得到两倍的灰度值。
如果是非线性相应,一些算法的准确度将会降级
- 如:亚像素精度阈值分割、灰度值特征提取
- 如果我们需要准确地测量就必须确定非线性相应并求其逆响应。
- 如果对非线性相应的图像使用了逆响应,那么结果图像就是线性相应的。
- 确定逆响应函数的过程就被称作辐射标定。
3.2.2.1 Chart-Based Radiometric Calibration 基于图表的标定法
- 传统的方法是采用经过标定的目标物(典型标定目标物是灰阶卡)来进行辐射标定
相应的算法被称为基于图表的标定算法
- 测量不同梯度的灰度值并将这些灰度值与这些梯度条已知的反射系数进行比较。
- 这种比较将产生一系列的独立测量。
- 通过这一组测量完成函数的拟合,如下式给出的包含增益和偏移的一个伽马相应函数:
$$f(g)=(a+bg)^{\gamma}$$

存在的问题
- 需要整个视野内有非常均匀的照明,再生产现场环境中难以实现。
- 晕影效应可能导致表面光向边界分散
- 标定板的格式没有被标准化
- 密度标定板的反射比通常是为各种照相应用定制的,这意味着反射系数与密度是线性级数相关的,密度与反射系数是对数相关的。
3.2.2.2 Chartless Radiometric Calibration 无图表辐射标定法
- 需要不适用标定板的辐射标定算法,称为无图表辐射标定
他们基于在不同曝光下对同一场景所拍摄的一系列图像来实现
- 不同的曝光给可以通过改变光圈,也可以通过改变曝光时长
优点:
- 不需要标定板
- 不需要在视野内有均匀的照明
- 所有可能的灰度值取值范围能够被多幅图像所覆盖
- 灰度值G是传感器在曝光过程中e所累积的能量E的一个非线性函数r
$$G=r(eE)$$ - e与曝光时间成比例,业余镜头入射光控面积成比例,即与$(1/F)^{2}$成比例
- 辐射标定的目的是确定逆响应$q=r^{-1}$
- 假设采用了不同的曝光$e_{1}$和$e_{2}$采集了两幅图像,则$G_{1}=r(e_{1}E)$且$G_{2}=r(e_{2}E)$,得到$q(G_{1})=e_{1}E$和$q(G_{2})=e_{2}E$,得到
$$\frac{q(G_{1})}{q(G_{2})}=\frac{e_{1}}{e_{2}}=e_{1,2}$$ - q只依赖图像的灰度值和曝光比值$e_{1,2}$
- 计算q的一个方法是将q离散到一个查找表中,这样$q_{i}=q(G_{i})$
- $\log(q_{1}/q_{2})=\log(e_{1,2})$
- 即$\log(q_{1})-\log(q_{2})=\log(e_{1,2})$
- 如果设定$Q_{i}=\log(q_{i})$,$E_{1,2}=\log(e_{1,2})$,则:
$$Q_{1}-Q_{2}=E_{1,2}$$ - 因此得到一个线性方程组$AQ=E$,此除Q表示对数逆响应函数的查找表,A是一个256列的阵列(对于8bit图像)
- 矩阵A和E的行数与图像中像素的个数相等
- AQ=E是overdetermined equation system超正方程组,可由normal equations正规方程组$A^{T}AQ=A^{T}E$求解.


- 为了推导出更快速的算法,此方程组的每个方程都存在下列形式:
$$*(0..010..0-10..0)Q=E_{1,2}$$ - 上式中1所在的位置与第一幅图像的灰度值相等,-1所在的位置与第二幅图像的灰度值相同
- 使用正规方程组意味着在A中出现k次的每一行在正规方程中的权都为k。
- 通过将这一对灰度值相应的行于$\sqrt{k}$相乘,并使该行尽在A中包含一次即可得到同样的结果
确定k最简单的方法是计算这对图像的二维直方图。
- 从二维直方图中可以得到第一幅图像中灰度值为i的那些像素在第二幅图象的同样位置上灰度值是j的情况所出现的频率
- 对于8bit图像,二维直方图是256*256的图像,横坐标表示第一幅图像上的灰度值,纵坐标表示第二幅图像上的灰度值
3.2.3 Image Smoothing 图像平滑
每幅图像都包含某种程度的噪声
- 噪声可堪为多种原因造成的灰度值的随机变化
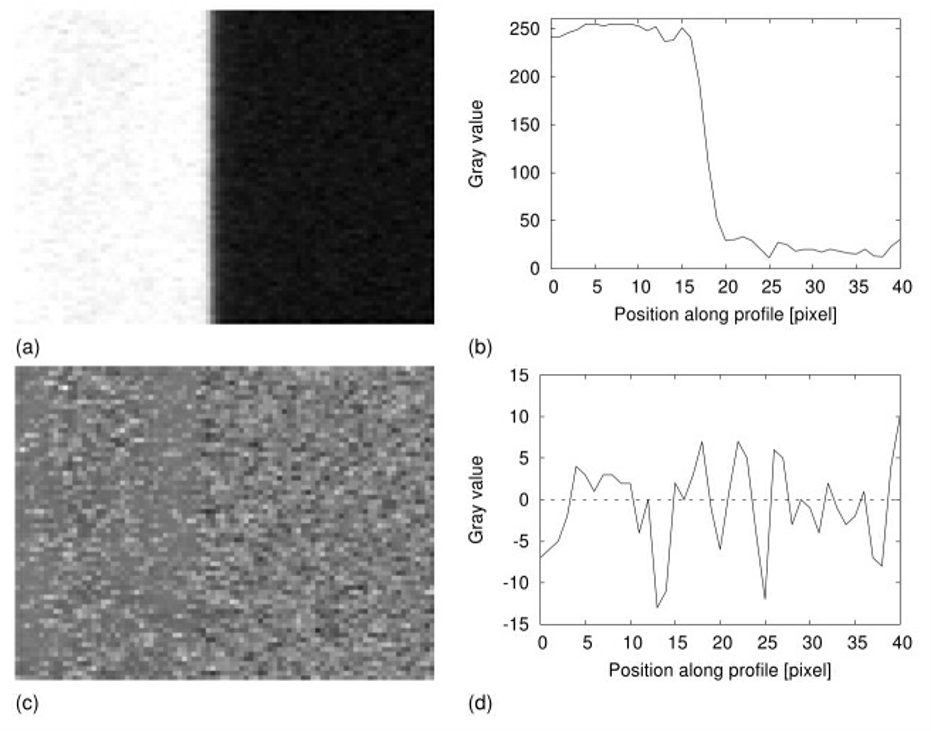
- 噪声可堪为多种原因造成的灰度值的随机变化
(b) 图像中心部分的水平灰度值剖面图
(d)噪声的水平灰度值剖面线
3.2.3.1 Temporal Averaging 时域平均值
噪声被视为一种平稳随机过程stochastic estimation problem
- 平稳:噪声与图像上像素的位置无关
- 真正的像素值$g_{r,c}$被一噪声项$n_{r,c}$干扰厚得到的灰度值:$g'_{r,c}=g_{r,c}+n_{r,c}$
- 采集同一场景的多幅图像平对这些图像进行平均,由于多幅图像实在不同时间采集的,此方法称为时域平均或时域平均值
- 采集n副图像:
$$g_{r,c}=\frac{1}{n}\sum_{i=1}^{n}g'_{r,c_{i}}$$ - 该降噪方法在X光检测系统中广泛引用
- $σ^{2}_{m} = σ^{2}/n$,噪声方差降低到了原来的$1/n$,标准偏差降低到原来的$1/\sqrt{n}$
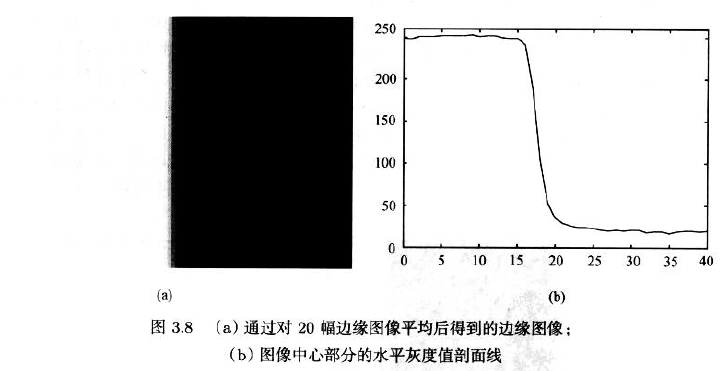
缺点:
- 必须采集多幅图像才能进行噪声抑制
3.2.3.2 Mean Filter 均值滤波器
- 空间平均或者空间平均值可以通过像素是(2n+1)*(2m+1)的一个窗口(也称作掩码)按如下方法计算:
$$g_{r,c}=\frac{1}{(2n+1)(2m+1)}\sum_{i=-n}^{n}\sum_{j=-m}^{m}g'_{r-i,c-j}$$
- 噪声的方差降低到了原来的$\frac{1}{(2n+1)(2m+1)}$
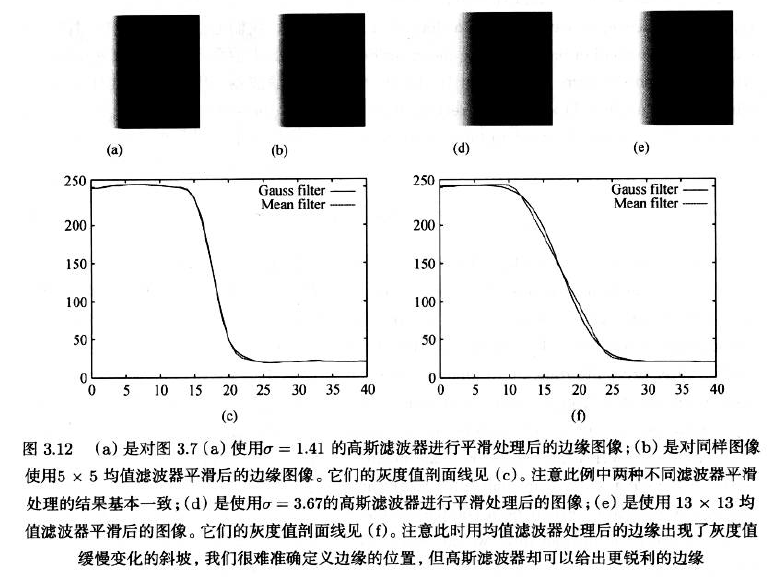
- 空间平均法平滑后的边缘不如时域平均法的锐利,空间均值滤波器使边缘模糊
- 同时忽略了图像在二维空间上有限的事实,如果掩码靠近图像边界,掩码会有部分靠近图像的外界
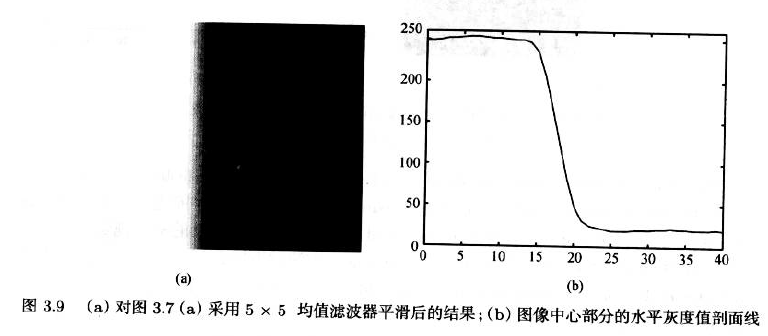
3.2.3.3 Border Treatment of Filters
解决方法:
只针对掩码能完全覆盖的图像内的像素进行滤波计算
- 图像缩小
将图像外的灰度值定义为0
- 像素越靠近边界越暗
图像边界意外的像素灰度值等于图像边界上最邻近的像素点的灰度值
- 在图像边界上产生原本不希望产生的边缘
以图像边界为中心,令图像外某位置上未定义的灰度值等于图像内其镜像位置的灰度值
- 最小程度地人为干扰
3.2.3.4 Runtime Complexity of Filters 运行时滤波器复杂度
- 每个像素需要进行(2n+1)(2m+1)次操作,对于w*h的图像,夫再度为$O(whmn)$
- 圆括号内包含的项只需要斤算一次且可以保存下来,比如保存到某一临时图像中。这意味着可以先计算输入图像在纵向上的和,并将此结果保存在一副临时图像中,然后再计算临时图像在横向上的和。
- 复杂度降低到$O(wh(m+n))$
- $$g_{r,c}=\frac{1}{(2n+1)(2m+1)}\sum_{i=-n}^{n}(\sum_{j=-m}^{m}g'_{r-i,c-j})$$
- 如果一个滤波器在运算时允许分别在行和列上求和,那么此滤波器称为可分滤波器 separable
- 圆括号内的部分有更佳的方法,用$t_{r,c}$来表示纵向的和,就有:
$$t_{r,c} = \sum_{j=-m}^{m}g'_{r,c-j}=t_{r,c-1}+g'_{r,c+m}-g'_{r,c-m-1}$$ - 该规则也适用于横向,这样总计算复杂度使$O(wh)$
- 只要某滤波器在运算时能采用此机制,即在前一个计算出的值上计算出新的值,这种滤波器叫做递归滤波器 recursive filter
- 滤波:一个采用某个函数作为输入并产生某个函数作为输出的操作
3.2.3.5 Linear Filters 线性滤波器
- 均值滤波器使线性滤波器中的一个例子
线性滤波器的特点:
- 应用一个滤波器到两幅输入图像的一个线性组合上所产生的结果,与对这两幅图像分别应用此滤波器后将结果按统一现行规则进行组合得到的结果完全一致。
- 用h来表示线性滤波器,f和g表示两幅图像,则有
$$h\{af(p)+bg(p)\} = ah\{f(p)\}+bh\{g(p)\}$$
- 线性滤波器可以通过卷积来计算,对于在连续域上的一维函数卷积操作如下:
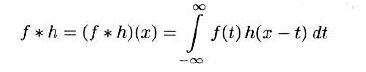
- f表示图像函数,滤波器h由另一函数确定,此函数被称为滤波器掩码filter mask的卷积核convolution kernel
- 对于二维函数:
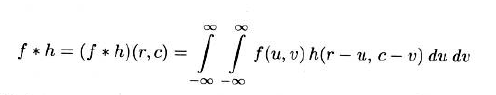
- 对于离散域上的函数,积分被求和取代
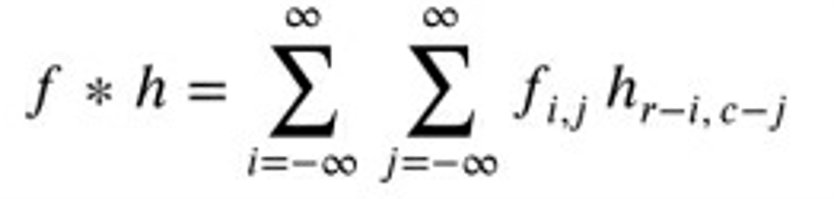
- 为了能够在有限时间内计算卷积,滤波器h在大于r和c的情况下必须为0
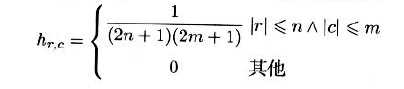
可分滤波器的概念可以被扩展到任意线性滤波器上。
- 如果$h(r,c)$能够被分解为$h(r,c)=s(r)t(c)$,h被称为可分的。
- 此是为更有效地实现均值滤波,可以提出因子$s$
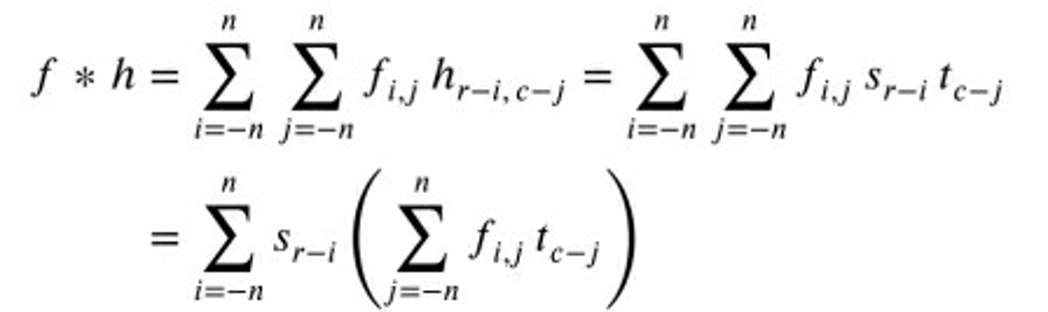
- 递归线性滤波器的应用同理
递归线性滤波器与均值滤波器的递归实现有着同样的速度优势,即运行时间与滤波器的尺寸无关。
- 很多常用滤波器不能以递归滤波器的方式实现,之恶能被近似为一个递归滤波器
3.2.3.6 Frequency Response of the Mean Filter 傅里叶变换
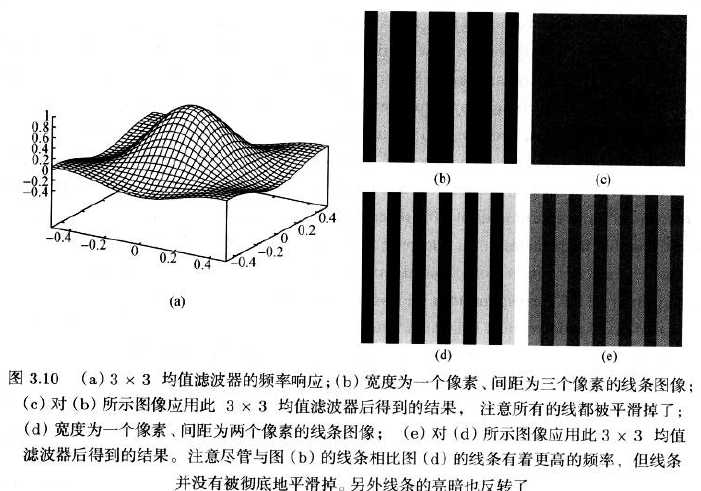
- 在此坐标图中,横坐标和纵坐标为0时对应的频率时0,这表示的是图像中可能出现的最高频率。
- 亮暗反转是由于频率响应中负值部分造成的
均值滤波器的频率相应不是旋转堆成的,是各向异性。
- 意味着倾斜方向上的结构与水平或垂直方向上的结构在应用同一滤波器时会经历不一样的平滑处理
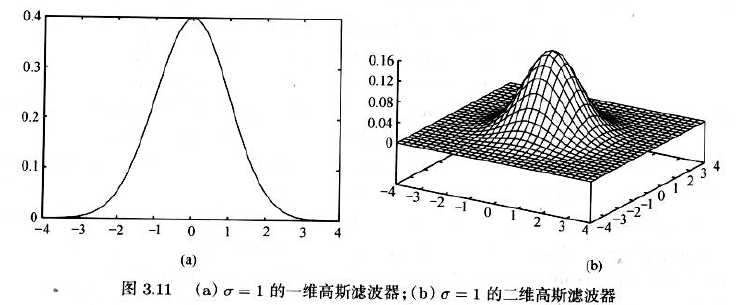
3.2.3.7 Gaussian Filter 高斯滤波器
理想的平滑滤波器
- 滤波器是线性的
滤波应与位置无关
- 无论物体出现在哪一个位置,都能产生同样的结果
- 旋转对称的,也是各向同性的
希望有一个参数t来控制平滑的程度
- t越大,平滑程度越大
- 高斯滤波器时唯一符合上述全部准则的滤波器
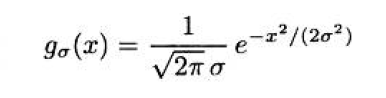
- 这个函数也描述了正态分布随机变量的概率密度。
- 二维高斯滤波器:
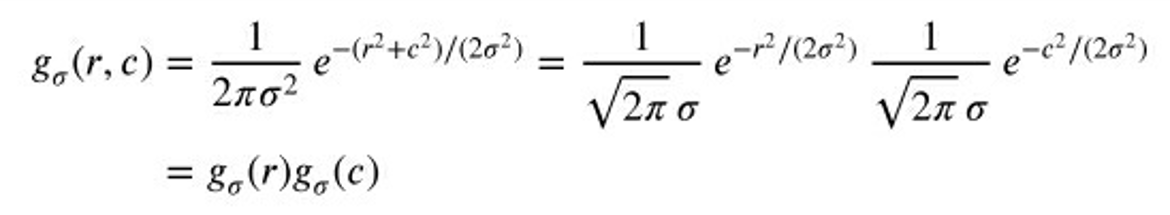
高斯滤波器时可分的,但不是递归的。
- 它是唯一的各向同性的可分平滑滤波器器
3.2.3.8 Noise Suppression by Linear Filters 线性滤波器的噪声抑制
- 任何线性滤波器都会改变图像所包含噪声的方差。
- 对于一个线性滤波器$h(r,c)$,噪声的方差将乘以如下倍数
- 对于高斯滤波器,这个倍数是$1/(4\piσ^{2})$
- 如果同一个n*n的均值滤波器相比,为了让高斯滤波器具有同样的噪声抑制效果,必须让$σ=(2n+1)/(2\sqrt{\pi})$
- 高斯滤波器产生了相对锐利的边缘
3.2.3.9 Median and Rank Filters 中值滤波器
- 中值被定义为在样本概率分布中50%的值小于此值,而另外50%的值大于此值
通过计算当前窗口内覆盖的像素的中值而不是平均值就得到一个中值滤波器
- 中值滤波器时不可分的
- 处理后的图像边缘是否会变化、变化的程度不能预先估计,不能估计出中值滤波器抑制噪声的程度。
3.2.4 Fourier Transform 傅里叶变换
3.2.4.1 Continuous Fourier Transform 连续傅里叶变换
一维函数的傅里叶变换
- 将函数h(x)从空间域到频率域的转换。
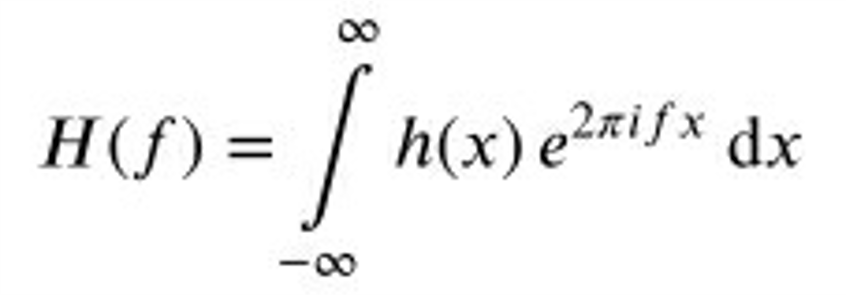
- 将函数h(x)从空间域到频率域的转换。
- 将位置x的函数h(x)转换到频率f的函数H(f),H(f)通常时复数。
- 可以认为h(x)是由不同频率和不同振幅的正弦和余弦波组成
- 从频率域到空间与的傅里叶逆变换由下式给出:
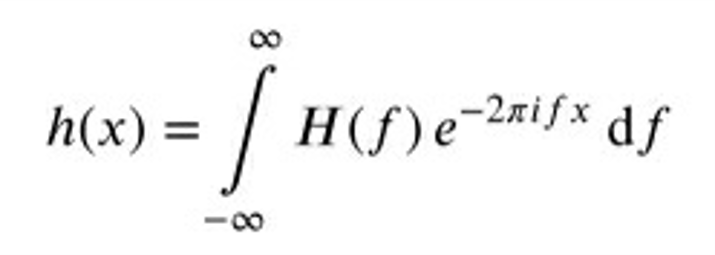
- 二维傅里叶变换和逆变换如下
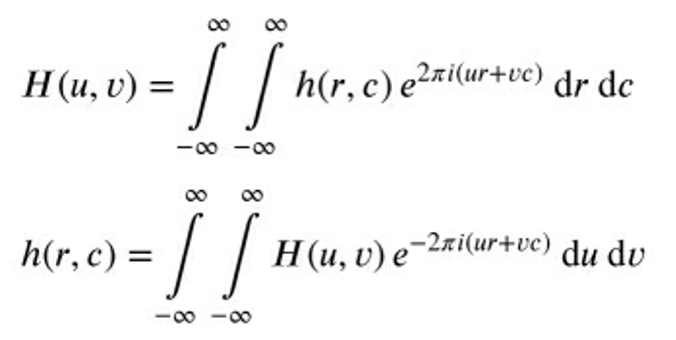
- 空间域的卷积被变换为在频率域的一个简单相乘: $$(g*h)(r,c) \leftrightarrow G(u,v)H(u,v)$$
- 因此通过将图像及使用的滤波器变换到频率域,将此二者在频率域转换的结果相乘厚再换回空间域就实现了卷积操作。
- 均值滤波器的傅里叶变换
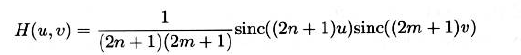
- 高斯滤波器的傅里叶变换
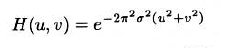
- $H(-u,-v) = \overline{H(u,v)}$
3.2.4.2 Discrete Fourier Transform 离散傅里叶变换
- 对于任意的正弦余弦波,可能出现的最高频率都是1/2,频率1/2被称为尼奎斯特临界频率Nyquist critical frequency
混淆现象
- 高于1/2频率的正弦或余弦看起来与相应的更低频率的正弦或余弦波一样。
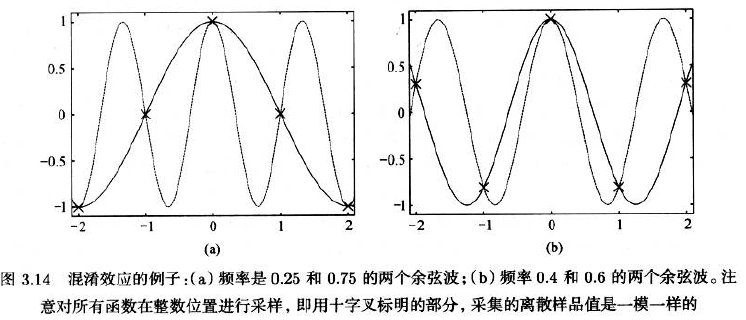
- 高于1/2频率的正弦或余弦看起来与相应的更低频率的正弦或余弦波一样。
为了消除频率混淆,在对图像进行采样前必须将高于尼奎斯特临界频率的高频部分消除。
- 可以通过摄像机的光学低通滤波镜实现。
在一副图像按比例缩小时也可能发生混淆现象。
- 对图像进行低分辨率采样前,先使用平滑滤波器以保证消除了所有高于尼奎斯特临界频率的高频部分时很重要的。
- 快速傅里叶变换FFT
使用傅里叶变换进行滤波的好处:
- 通过使用定制的滤波器来消除图像中某些特定的频率

- 通过使用定制的滤波器来消除图像中某些特定的频率
评论已关闭