机器视觉-Chapter 3.3 Geometric Transformations 几何变换
3.3 Geometric Transformations 几何变换
3.3.1 Affine Transformations 仿射变换
- 如果在机械装置上物体的位置和旋转角度不能保持恒定,我们必须对物体进行平移和旋转角度修正。有时由于摄像机和物体间的距离发生了变化,导致图像中物体的尺寸发生了明显变化。这些情况下使用的变换称为仿射变换,可以用以下等式描述:
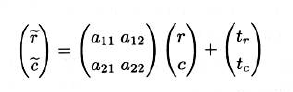
- 一个仿射变换包括一个由2*2矩阵给定的线性部分和一个平移部分
- 简化后:
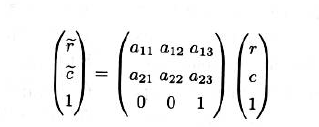
- 这种附加了多余的第三个坐标的标识发叫做齐次坐标,原先的坐标叫做非齐次坐标
- 任何仿射变换都能由以下基本变换构造而来,此除基本变换矩阵的最后一行已被省略
- 倾斜是仅让一个轴旋转

3.3.1.1 Projective Transformations 投影变换
仿射变换几乎能校正物体所有可能发生的与位姿相关的变化。
- 如果讨论的物体在三维空间发生了旋转,它就经历了一个很平常的投影变换,由于可能出现阴影或遮挡,此投影变换很难修正。
- 如果物体是平面的,能通过二维投影变换对此物体的三位变换进行模型化

- 仿射变换是特殊的投影变换
- $w=0$的点被称为无限点,因为他们位于某一方向上无限远处
- $w\neq0$的点被称为有限点
一个投影变换由八个独立参数,那么投影变换就可以通过四个相应的点被唯一地确定
- 从图上取四个点,典型情况下是一个举行,然后矫正图像使得这四个被提取出来的点能变换到矩形的四个角上
3.3.2 Image Transformations 图像变换
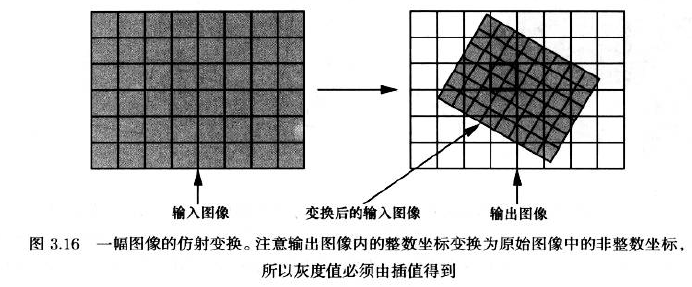
3.3.2.1 Nearest-Neighbor Interpolation 最近邻域插值法
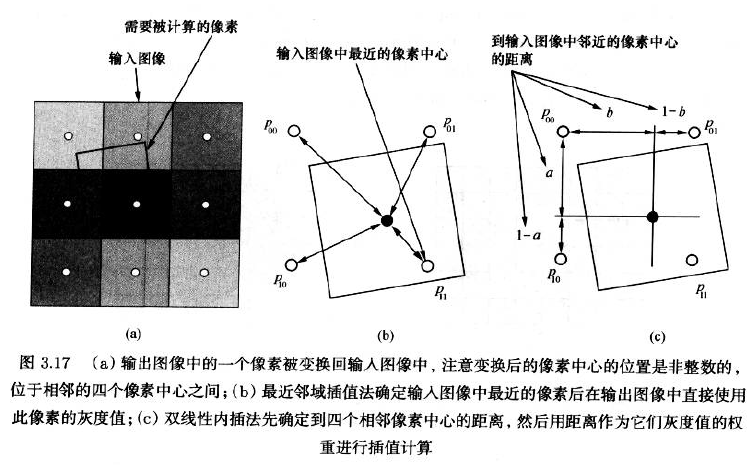
- 先对转换后像素中心的非整数左边进行取整处理,以找到与此坐标相邻四个像素点中心位置最近的一个,然后将输入图像里的这个最邻近位置的像素灰度值视为输出图像内相应像素点的灰度值
最近邻域插值法的结果会出现锯齿状外观
- 原因:把图像看成了分段函数
- 原因:把图像看成了分段函数
3.3.2.2 Bilinear Interpolation
- 使用适当的权重配合四个灰度值进行插值计算,称为双线性插值法
- 首先分别计算转换后的坐标到四个相邻像素中心点的垂直和水平方向的距离,然后根据不同灰度值所占的权重计算。

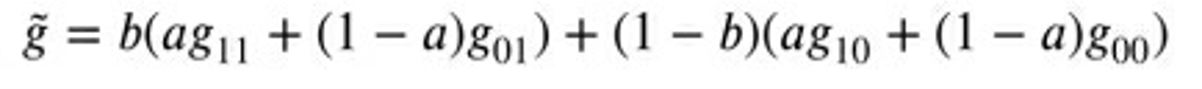
3.3.2.3 Bicubic Interpolation 双三次

3.3.2.4 Smoothing to Avoid Aliasing
- If we scale down an image, we are subsampling it对其二次采样.
- As a consequence, we may obtain aliasing effects混淆现象.

3.3.3 Projective Image Transformations 投影图像变换

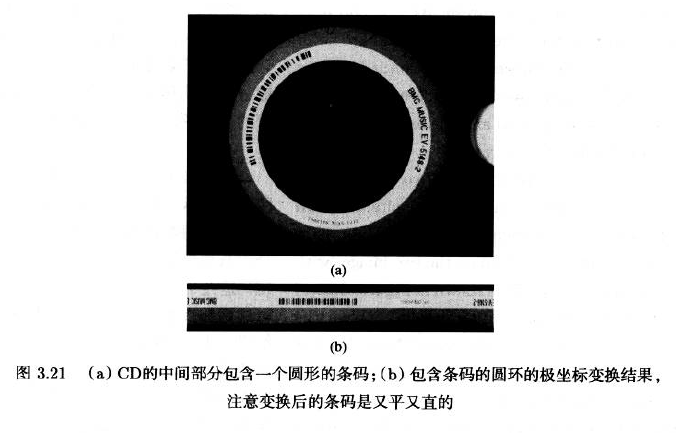
3.3.4 Polar Transformations 极坐标变换
- 极坐标变换通常用来矫正图像中的圆形物体或被包含在圆环中的物体
- 变换中心$(m_{r},m_{c})$

- 逆变换
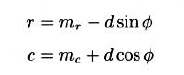
评论已关闭