3.4 Image Segmentation 图像分割

3.4.1 Thresholding 阈值分割

3.4.1.1 Global Thresholding全局阈值

  • 阈值分割操作定义为：

    • 102.png
  • 经常使用$g_{min} = 0$或$g_{max}=2^{b}-1$
  • 如果光照能保持恒定，阈值$g_{min}$和$g_{max}$能在系统设置时被选定且永远不用被调整。
  • 103.png

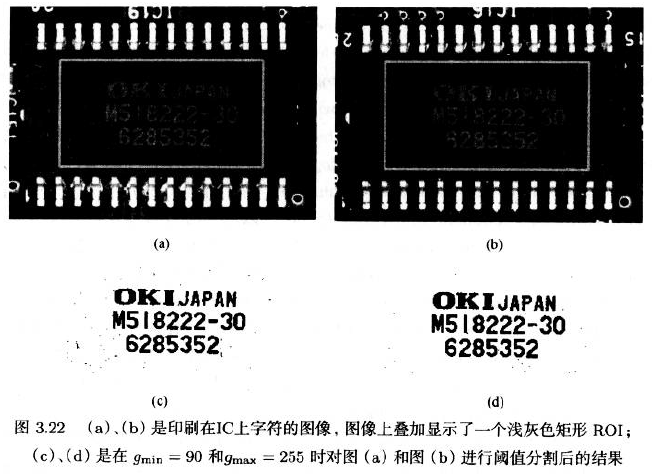
  • 固定阈值仅在物体的灰度值和背景灰度值不变时效果很好

    • 照明变化后物体的背景的灰度值就会发生变换
    • 即便使用的照明是恒定的，相似物体间不同的灰度值分布也会使固定阈值分割的结果不理想。

3.4.1.2 Automatic Threshold Selection自动阈值分割

  • 一个好的阈值应该是对应直方图中的两个峰之间的最小值，不幸的是，由于灰度值在直方图中的随机波动，两个峰尖的最大值和他们之间的谷底最小值都不能被很好的确定

    • 灰度值小的峰是背景，大的是IC上的字符
  • 希望以鲁棒的方法选定对应阈值，先对直方图进行平滑处理
  • 逐渐增大高斯滤波的σ值平滑直方图
    104.png

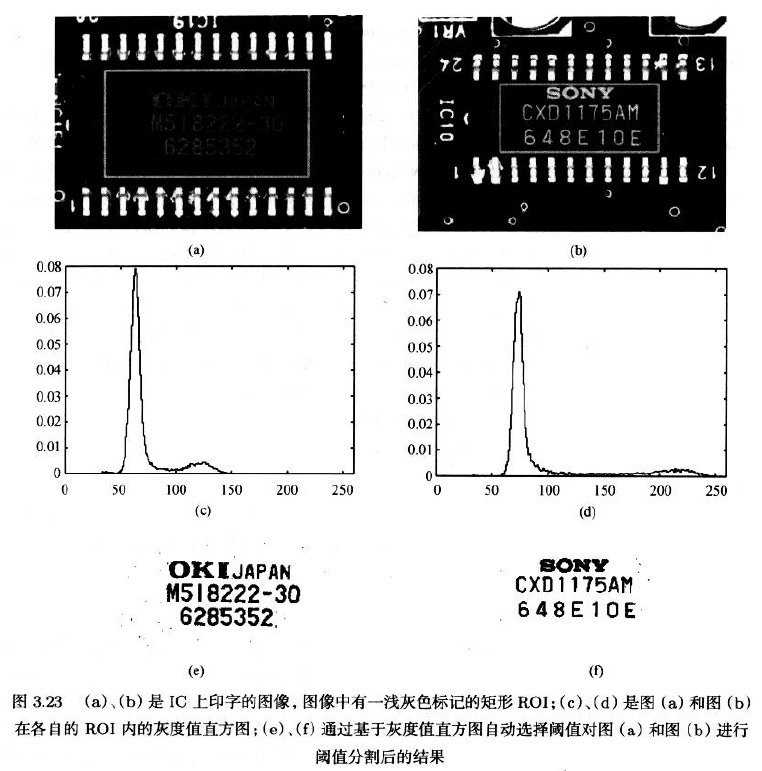
  • 若直方图存在双峰的条件不满足时，该方法就不好了

    • 不均匀照明是导致该情况的另一个原因
    • 但是在局部区域中感兴趣的物体经常要比背景更暗或更亮

105.png

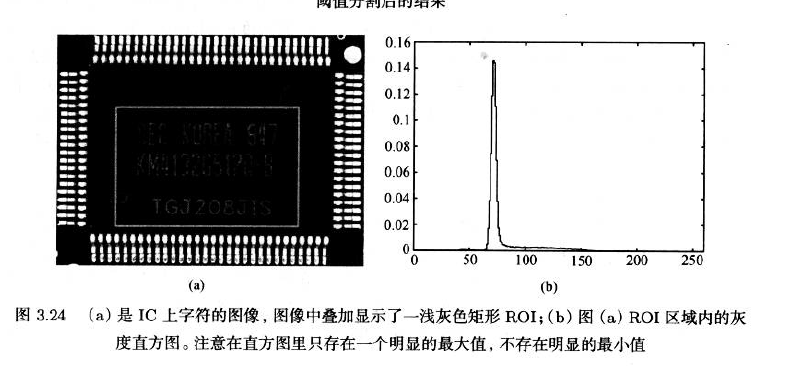
3.4.1.3 Dynamic Thresholding动态阈值

  • 因此希望指定一个像素必须比其所处的背景亮多少或暗多少
  • 唯一的问题是如何确定局部区域的背景灰度值
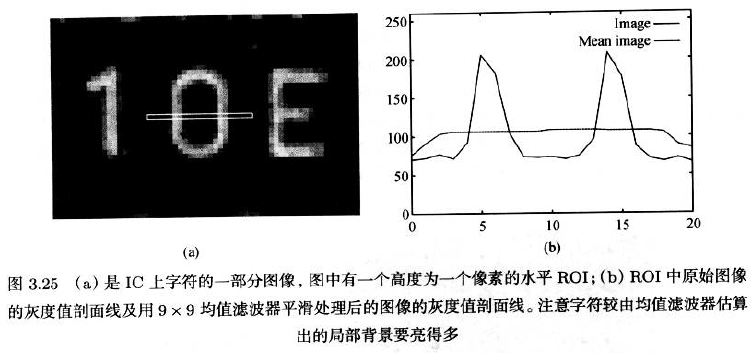
  • 使用均值/高斯/中值滤波器进行平滑处理就可以计算出以当前像素为中心的窗口内的平均灰度值，所以可以使用输出结果作为对背景灰度值的估计。
  • 将图像与其局部背景进行比较的操作被称为动态阈值分割处理。

  • $f_{r,c}$表示输入图像，$g_{r,c}$表示平滑后的图像，则对亮物体的动态阈值分割处理如下：

    • 106.png

  • 对暗物体的动态阈值分割处理如下：

    • 107.png

  • 如果滤波器的尺寸太小，那么在物体中心估计出的局部背景将不理想。

    • 凭经验，均值滤波器的宽度必须大于被识别物体的宽度

108.png

3.4.1.4 Variation Model 变差模型、差异模型

  • 动态阈值分割可以用来检测某一物体上的缺陷，$g_{r,c}$被称为参考图像
  • 待测物体$f_{r,c}$和参考图像$g_{r,c}$必须精准地对准
    109.png
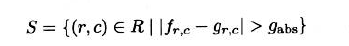
  • 此类动态阈值分割处理对物体的形状要求很严格
  • 为了改善算法，在进行阈值分割处理时，要考虑图像中的期望灰度值偏差,用$v_{r,c}$表示灰度值容许的偏差。理想情况下，将分割出与参考图像的偏差大于容许偏差的那些像素

110.png

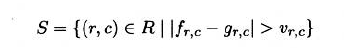
  • 可以从n幅图像训练,n幅图像的平均值和标准差如下:

111.png

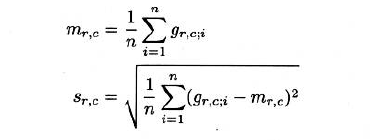
  • 图像$m_{r,c}$可以用来模型化参考图像,$s_{r,c}$则可以来模型化参考图像的容许偏差
  • 称此方法为偏差模型法
  • 理想情况下通过标准差与一个小倍数$c$相乘得到$v_{r,c}$,$v_{r,c} = cs_{r,c},c=3$

  • 如果一组训练图像的偏差非常小

    • 如:训练图像噪声小于检测的图像
  • 或者由于物体的一部分接近摄像机的饱和极限时,此方法不好
  • 这些情况下,引入一个绝对阈值$a$,使得$v_{r,c}=max(a,cs_{r,c})$
  • 这样偏差阈值对于$m_{r,c}$就不再是对称的,需要为太亮或太暗的像素引入两幅阈值图像
  • 用$u_{r,c}$和$l_{r,c}$表示阈值图像,a和b表示绝对阈值

112.png
113.png

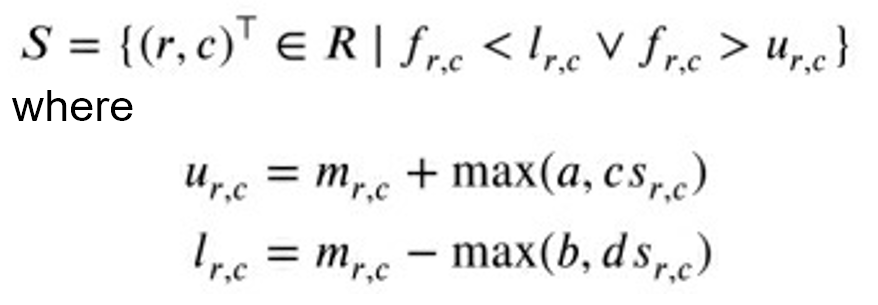
  • 对于只采集一幅参考图像,建立偏差模型的方法:

    • 人为创建一些偏差
    • 当允许尺寸和位置存在小的公差时,在物体边缘就存在着相应的中最大偏差,可推导出偏差模型

3.4.2 Extraction of Connected Components 提取连通区域

  • 为获得每一个区域,必须计算出分割后所得到的区域内所办含的所有联通区域

  • 在一个矩形像素网格上,对于连通性有两种自然定义:

    • 这两个像素有共同的边缘,称为4连通 4-connectivity或4邻域 4- neighborhood
    • 将对角线上的相邻像素也包括进来,称为8连通 8-connectivity或8邻域 4- neighborhood

114.png

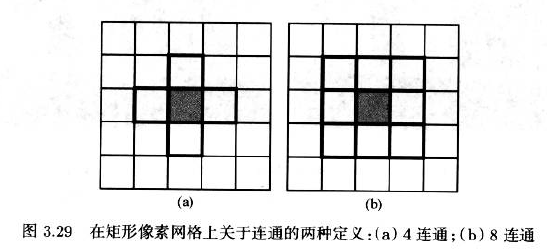
  • 对前景和背景都使用同一个定义是,会出现问题

    • 解决此问题的唯一方法是对前景和背景使用不同的连通性定义
      115.png

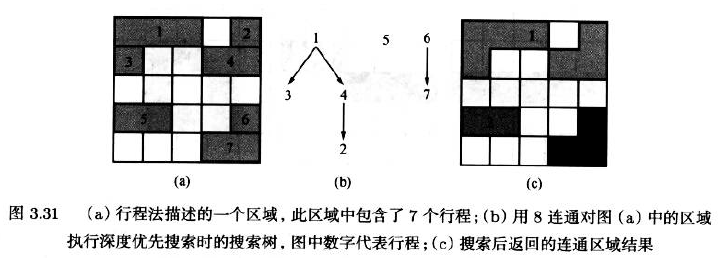
  • 反复搜索第一个未被处理的行程,然后在与此行程相邻的上下两行中搜索与此行程交叠的所有行程.

    • 判断两个行程是否交叠的依据就是连通性的定义

116.png

3.4.3 Subpixel-Precise Thresholding 亚像素精度阈值分割

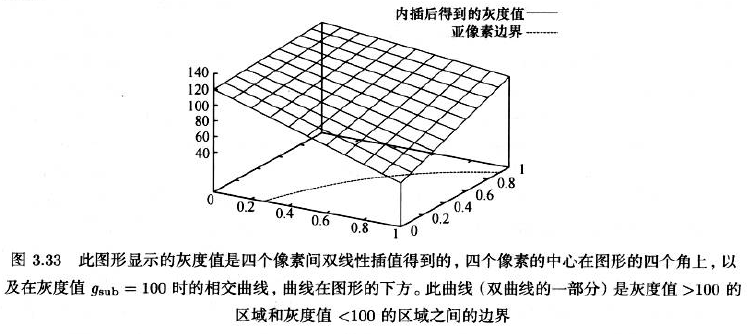
  • 亚像素精度阈值分割处理的结果不能是一个区域,因为区域是像素精度的

  • 表示结果的适当数据结构应该是亚像素精度轮廓

    • 此轮廓表示图像中两个区域之间的边界
    • 这两个区域中一个区域的灰度值大于灰度值阈值$g_{sub}$而另一个区域的灰度值小于$g_{sub}$

    • 为了获取这个边界,必须将图像的离散表示转换成一个连续函数

      • 可通过双线性插值
        120.png

117.png
118.png
119.png

标签: 机器视觉, 图像分割

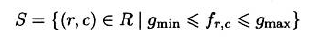
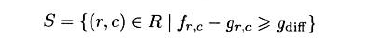
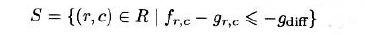
评论已关闭