3.6 Morphology 形态学

3.6.1 Region区域 Morphology

3.6.1.1 Set集合 Operations

  • 并集

    • 140.png
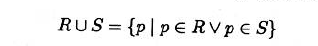
    • 可交换性 可结合性

  • 交集

    • 141.png
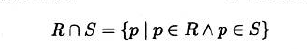
    • 可交换性 可结合性

  • 差集

    • 142.png
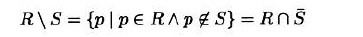
    • 不可交换 不能结合

  • 补集

    • 143.png
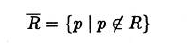
    • 由于一个有限区域的补集是无限的,不能用二值图像表示
    • 对于二值图像表示的区域,定义不含补集的操作是很重要的

    • 行程编码表示的区域可以使用补集

      • 通过增加一个标记表示保存的是区域还是区域的补集

  • 平移向量$t$

    • 144.png

  • 一个区域的转置被定义为关于原点的一个镜像

    • 145.png
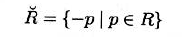
    • 转置是唯一需要挑选特殊点(原点)的操作,其他操作都不依赖于坐标系的原点,是平移不变的

3.6.1.2 Minkowski Addition and Dilation 闵可夫斯基加法与膨胀

  • R表示想处理的区域

  • S表示结构元

    • 通过结构元来描述感兴趣的形状.

  • 闵可夫斯基加法

    • 146.png
    • 147.png
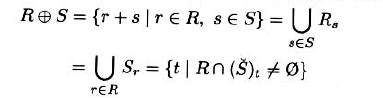
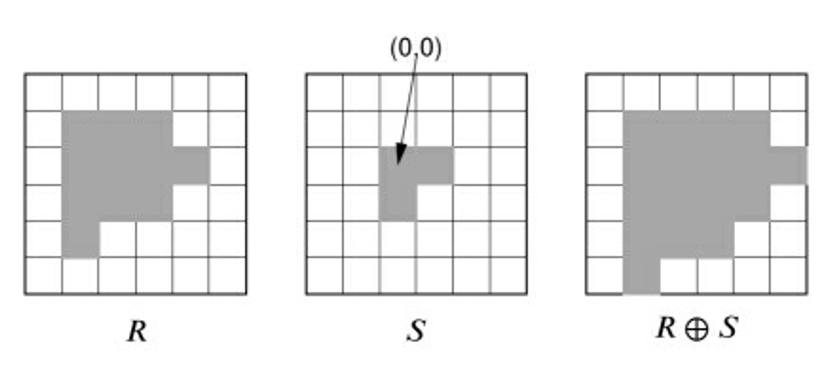
    • 转置后结构元至少与区域存在一个公共点
    • 可交换性 可分配性

  • 膨胀

    • 148.png
    • 149.png
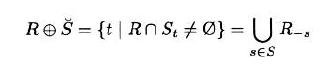
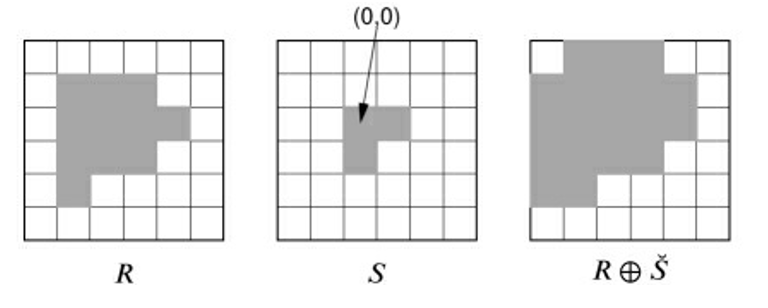
    • 只要结构元相对于原点是非对称的,那么闵可夫斯基加法和膨胀的结果是不一样的
    • 如果结构元是对称的,那么结果一样

150.png

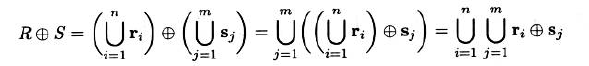
  • 可以用来将区域中彼此分开的几个部分合并成一个单一的部分,得到正确物体的连通区域
    151.png

3.6.1.3 Minkowski Subtraction and Erosion

  • 闵可夫斯基减法

    • 152.png
    • 153.png
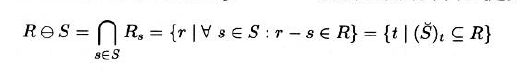
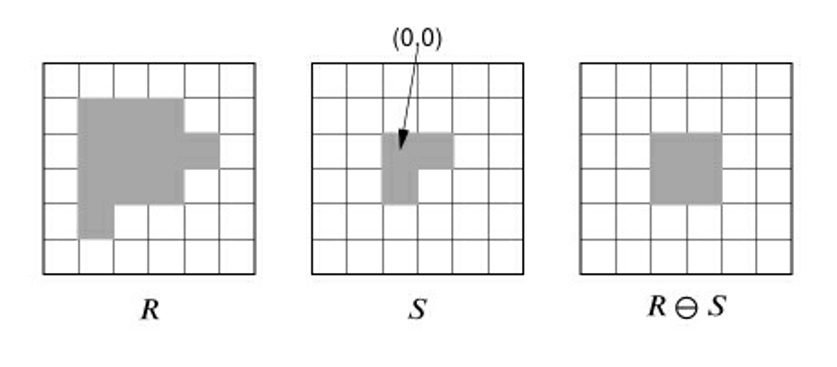
    • 结构元必须全部落在区域内
    • 转置结构元必须完全落在区域内

  • 腐蚀

    • 154.png
    • 155.png
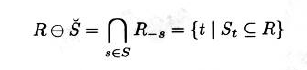
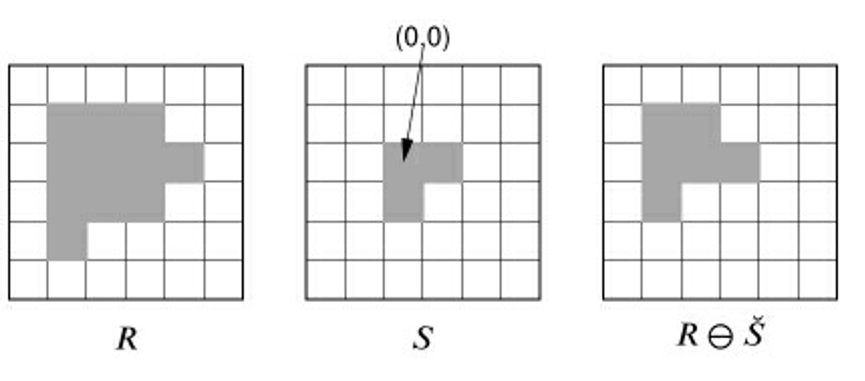
    • 只要结构元相对于原点是非对称的,那么闵可夫斯基减法和腐蚀的结果是不一样的
    • 很多情况下默认结构元是以原点为中心对成的,此时腐蚀就被定义为闵可夫斯基减法
  • 闵可夫斯基减法和腐蚀会将输入区域收缩,可以用来将彼此相连的物体分开
  • 156.png
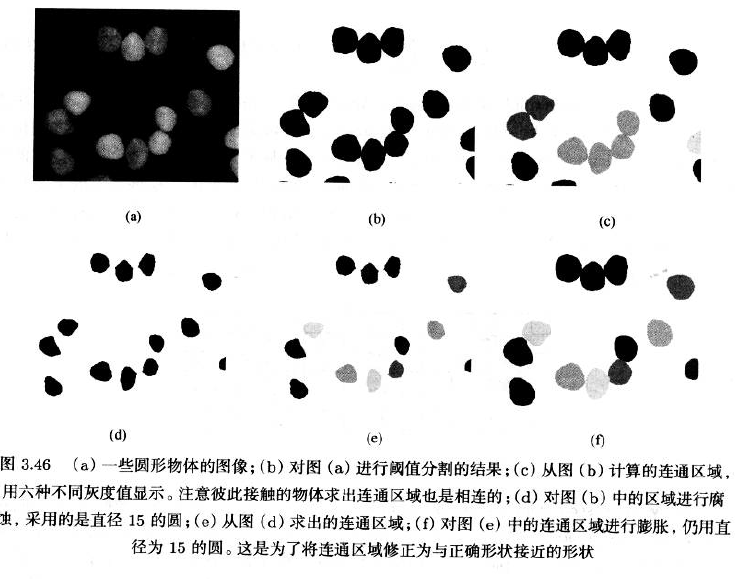
  • 采用腐蚀处理时使用的结构元对联通区域进行膨胀处理

  • 腐蚀操作返回的时对结构圆S评议后得到的参考点,这些点是每次平移后的结构元$S_{t}$彻底落在区域R内时得到的

    • 因此腐蚀处理的行为类似于模板匹配
  • 157.png

  • 闵可夫斯基加法和闵可夫斯基减法

    • 在进行补集操作时,他们彼此之间是互为对偶的
    • 158.png
    • 同样的等式适用于膨胀腐蚀
    • 对偶性dual仅限于补集是无限的情况下,不适用于二值图

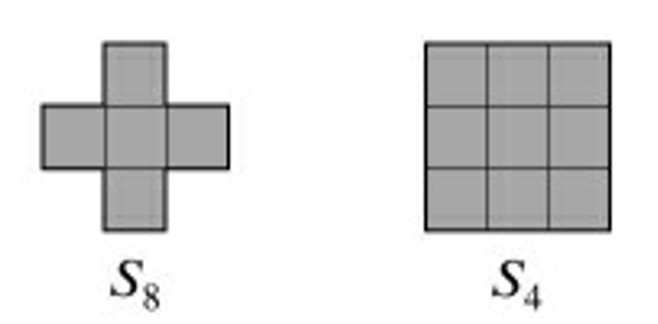
3.6.1.4 Region Boundaries

  • 腐蚀和膨胀最有用的应用是计算区域的边界

  • 计算内边界:

    • 对区域进行适当的腐蚀,然后从原区域减去腐蚀后的区域
    • 159.png

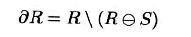
  • 计算外边界:

    • 膨胀处理后减去原区域
    • 160.png

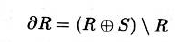
  • 得到8-连通的边界

    • 使用$S_{8}$结构元

  • 得到4-连通的边界

    • 使用$S_{4}$结构元
  • 161.png
  • 162.png

3.6.1.5 Hit-or-Miss Transform击中和不击中变换

  • 腐蚀能够被当作模板匹配,但是选择性不够

    • 腐蚀不考虑背景
    • 需要一个能将背景明确模型化的方法
  • 采用一个包含两个部分的结构元$S=(S^{f},S^{b})$,其中$S^{f} \cap S^{b} = \varnothing$

  • 击中-不击中变换定义为:

    • 163.png
  • 前景结构元$S^{f}$彻底地落在前景内,而背景结构元S^{b}彻底落在背景内

  • 击中-不击中变换与自身是对偶的

    • 164.png
  • 如只想匹配字母o
    165.png

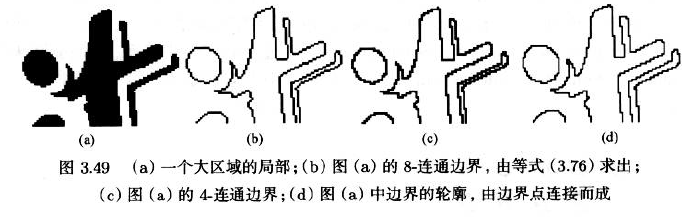
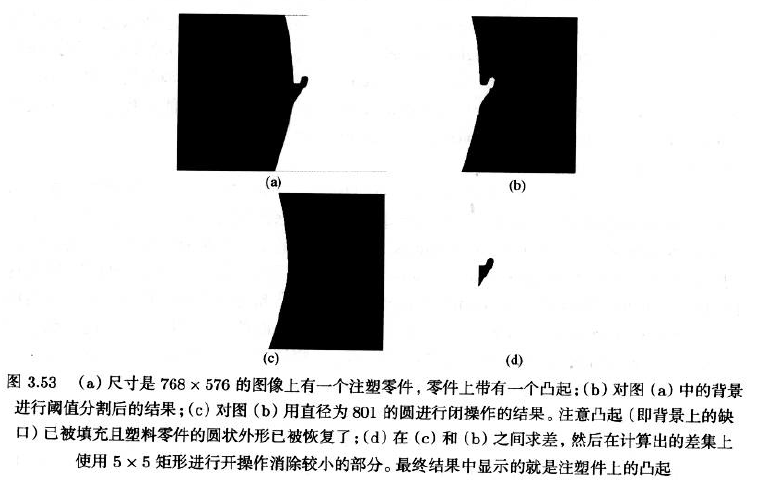
3.6.1.6 Opening and Closing开操作和闭操作

  • 开操作

    • 166.png
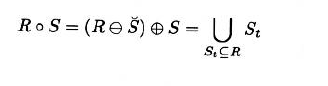
    • 先进行腐蚀,再使用同一个结构元的闵可夫斯基加法
    • 开操作相对于结构元是平移不变的

    • 与腐蚀操作/膨胀操作相比,开操作是幂等的

      • 168.png

    • 开操作能被用于模板匹配,与击中-击不中相比,它返回输入区域中能被结构元覆盖的全部的点.因此它保保持了要搜索的物体的形状

      • 169.png

      • 为了只找到o,可以组合击中-击不中开操作

        • 170.png

    • 如果使用类似圆形或矩形的结构元,那么区域中比结构元效地部分都会被从区域中去掉

      • 用于从区域中去除不想要的附加物
      • 也能用于去除边界上突出的部分以达到平滑区域边界的目的
      • 去除物体间相连的部分以达到分开物体的目的
      • 抑制小物体
    • 171.png

  • 闭操作

    • 167.png

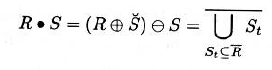
      • 先进行膨胀操作后再用同一个结构元进行闵可夫斯基减法
    • 172.png
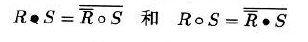
    • 闭操作相对于结构元也是平移不变的,也是幂等的
    • 闭操作和开操作是对偶的
    • 可以用来合并彼此分开的物体,这些物体间的间隙小于结构元
    • 使用类似圆或者矩形作为结构元,能够用来填充孔洞
    • 消除较结构元小的缺口
    • 平滑区域边界
    • 173.png

3.6.1.7 Skeleton 骨架

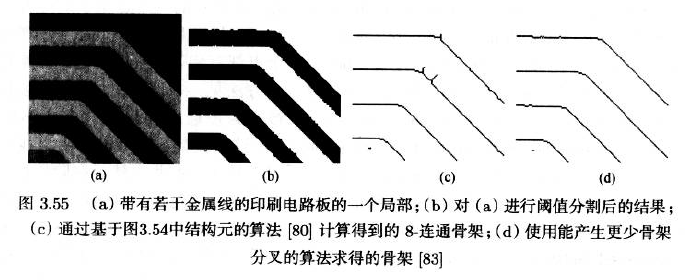
  • 如果物体几乎是线状的,即物体区域的长度比宽度大很多时,设法得到物体的中心线,就可以获得更直观的描述,这条中心线称为骨架或区域中轴

    • 骨架也可定义为所有极大远心的集合
    • 用于计算8-连通骨架的一组结构元见下图.使用这些结构元在全部四个可能的方向上反复进行击中-不击中变换,找到击中时的参考点,并将这些点从此区域内删除.不断迭代.
  • 175.png

3.6.1.8 Distance Transform距离变换

  • 距离变换返回的是一幅图像而不是一个区域,此图像的像素值是距离,这些距离代表的是区域R内每一个点到区域外所有点的距离的最小值.

    • 边界上所有点的距离都是1

    • 区域内其他点,距离要考虑在像素网格上的路径

      • 如果使用4-连通时,相应的距离称为4-连通距离

        • 176.png

      • 如果使用8-连通时,相应的距离称为8-连通距离

        • 177.png

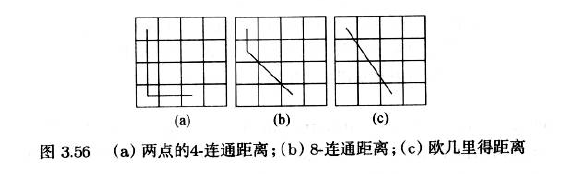
      • 欧几里得距离

        • 179.png
          178.png

  • 距离变换算法

    • 初始化:区域外所有的距离值是0,居于内所有的距离值是一个选定的最大距离值$2^{b}-1$,b是距离图像的像素位数

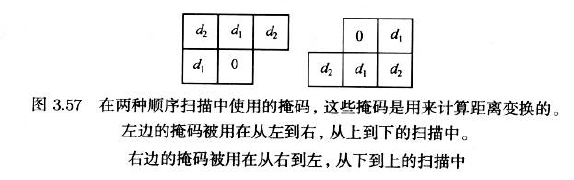
    • 在全图上进行两种顺序的扫描

      • 从左上到右下
      • 从右下到左上
    • 每一种扫描情况下,在当前像素放上掩码,将掩码覆盖区域中已有的距离值与掩码中此位置的元素相加,然后再从掩码中所有计算结果中选择最小的一个值作为当前像素的距离值.
    • 当$d_{1}=1 且 d_{2}=∞$时,计算的是4-连通距离
    • 当$d_{1}=1 且 d_{2}=1$时,计算的是8-连通距离
      • 当$d_{1}=3 且 d_{2}=4$时,除以3是近似欧几里得距离,称为chamfer-3-4距离
    • 180.png
      181.png

3.6.2 Gray Value Morphology 灰度值形态学

3.6.2.1 Minkowski Addition and Dilation 闵可夫四加法和膨胀

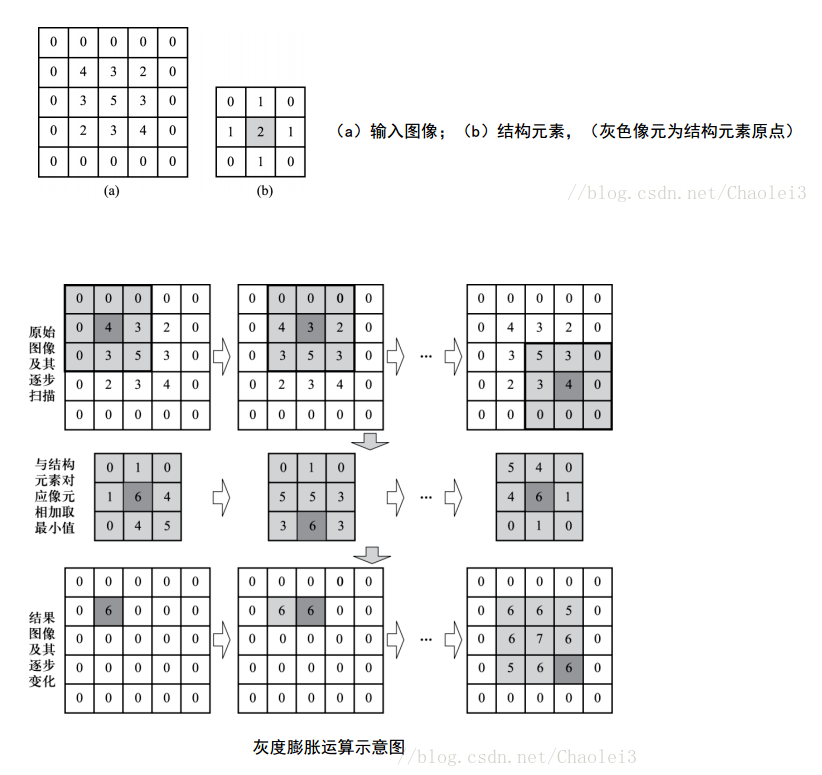
  • 用$g(r,c)$表示要被处理的图像,用$s(r,c)$表示ROI是S的一幅图像,s被称为结构单元

  • 闵可夫斯基加法定义为:

    • 182.png

  • 如果一幅图像在ROI S内的灰度值都是0时,则闵可夫斯基加法可变为:

    • 183.png

  • 膨胀能通过转置结构元来实现

    • 184.png

  • 灰度值形态学中,对结构元的选择通常是平坦结构元 flat structuring element

    • 对于$(r,c)∈S$时,$s(r,c)=0$

    • 这样灰度膨胀与区域膨胀的效果相似:

      • 扩大图像中比周围更亮的部分

    • 而且收缩背景:

      • 收缩图像中比周围更暗的部分
  • 灰度值膨胀被用来将灰度值图像中一个亮物体的脱节部分连在一起
  • 在仅使用区域操作不能轻松地将物体分割出来时,灰度值膨胀是有用的
  • 反之,灰度值膨胀能够将暗物体分裂
    185.png

3.6.2.2 Minkowski Subtraction and Erosion 闵可夫斯基减法和腐蚀

  • 闵可夫斯基减法

    • 186.png

  • 腐蚀

    • 187.png

  • 灰度值腐蚀收缩前景,扩大背景

    • 分开相互连接的亮物体
    • 连接支离破碎的暗物体

  • 对偶性

    • 补集操作:

      • $\overline{g_{r,c}} = 2^{b}-1-g_{r,c}$
    • 188.png

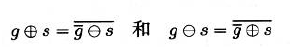
  • 当使用平坦结构元时,膨胀和腐蚀操作也能被视为两种特殊的滤波器

    • 在结构元范围内选择灰度最小值和最大值
    • 结构元可以视为滤波器掩码
    • 所以膨胀和腐蚀有时也被称为最大值滤波和最小值滤波

3.6.2.3 Opening and Closing

  • 开操作

    • 先腐蚀再执行闵可夫斯基加法
    • 189.png

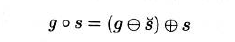
  • 闭操作

    • 先膨胀再执行闵可夫斯基减法
    • 190.png
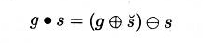
  • 对偶性

  • 能够被用来:

    • 填充小孔洞
    • 删除小物体
    • 连接或分开物体
    • 平滑物体的内外界
      192.png

191.png

3.6.2.4 Morphological Gradient 形态学梯度

  • 形态学梯度算子

    • 能够计算得到出现在结构元内的灰度值范围
    • 193.png

194.png

标签: 机器视觉, 形态学

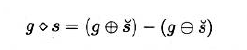
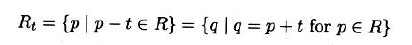
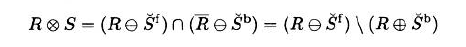
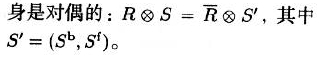
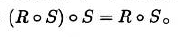
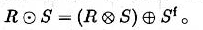
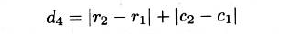
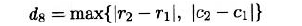
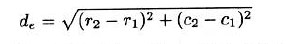
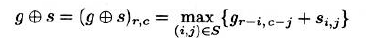
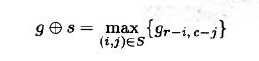
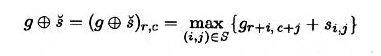
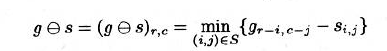
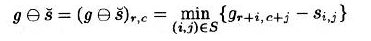
评论已关闭