3.3 Geometric Transformations 几何变换

3.3.1 Affine Transformations 仿射变换

  • 如果在机械装置上物体的位置和旋转角度不能保持恒定，我们必须对物体进行平移和旋转角度修正。有时由于摄像机和物体间的距离发生了变化，导致图像中物体的尺寸发生了明显变化。这些情况下使用的变换称为仿射变换，可以用以下等式描述：
    88.png

- 阅读剩余部分 -

3.2 Image Enhancement

3.2.1 Gray Value Transformations 灰度变换

  • 调整图像灰度值的一个原因是由于图像对比度太弱，这个问题通常只会局部发生，只需增强局部的对比度；

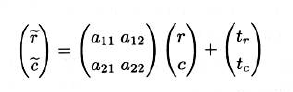
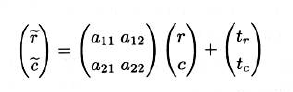
  • 另一个原因是图像的对比度或者亮度同最初系统设定时相比已经发生了变化

    • 如：工作一段时间后由于光源的老化而造成图像对比度变弱

  • 灰度值变换可以被视为一种点处理。

    • 这意味着变换后的灰度值$t_{r,c}$仅仅依赖于图像上同一位置的原始灰度值$g_{r,c}:t_{r,c}=f(g_{r,c})$。$f$表示进行灰度值变换的函数，其值域范围通常是$G_{b}$，为离散的。
    • 灰度值变换通常通过查找表（lookup table,LUT） 进行，即将每个输入灰度值变换后得到的输出值保存在这个查找表内。

- 阅读剩余部分 -

3.1 Fundamental Data Structures

3.1.1 Images 图像

  • 黑白摄像机返回每个像素对应的一个采样结果，并由此组成一幅单通道灰度图像。RGB彩色摄像机返回每个像素对应的三个采样结果，并由此组成一幅三通道图像。图像可被视为由一组任意多的通道组成。
  • 在某些应用领域中，比如遥感图像，图像的每个像素对应非常多的能量采样结果，这样做的目的时对光谱进行更细致的采样，所以每个像素对应更多个能量样本也是可以的。
  • 图像通道可以被简单看作一个二维数组。图像可以看作一个在空间上采样的函数，或者无限连续域上的函数。
  • 多数情况下，灰度值将被离散化为8位
  • 出于理论上的考虑，有时候为了方便会将图像视为无限连续域上的函数，即$f:R^{2}→R^{n}$

- 阅读剩余部分 -

2.1 Illumination照明

2.1.1 Electromagnetic Radiation

  • 电磁辐射：伽马射线 < X射线 < 紫外线 < 可见光 < 红外线 < 微波 < 无线电波。
  • 黑体：一个理想的辐射源，只释放自己的电磁辐射，而不会反射或透射其它辐射源的电磁辐射。
  • 光谱辐射：单位面积的黑体在单位立体角内、单位波长内辐射出的能量。

195.png

- 阅读剩余部分 -

  1. 1
  2. 2
  3. 3